
Place Value: It’s a Binary World page 5
F Razo CSUEB
TEACHING DIFFERENT NUMBER BASES
Up to now, and almost exclusively, teaching to count and manipulate quantities in K-12 classrooms has been focused on the Base 10 system. How appropriate is this for today's and tomorrow's needs?
Understandably, a focus on the Base 10 system has been critical in educating citizens to operate competently in a decimal world, even today. But with our world moving into automated measurement and calculation everywhere, the abilities to design, produce, and apply corresponding tools can very well define the future industrial and commercial success and dominance of organizations and nations. Because it seems that these abilities begin to be developed into our minds and bodies during the earlier years in our lives, perhaps it is a good time to rethink this issue in the context of our basic elementary education, so the foundations for basic modern number and computation concepts are properly laid when it is more effective.
What would it take to incorporate the topic of bases other-than-10
in the K-12 curriculum?
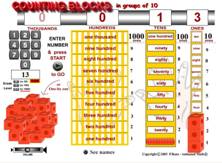
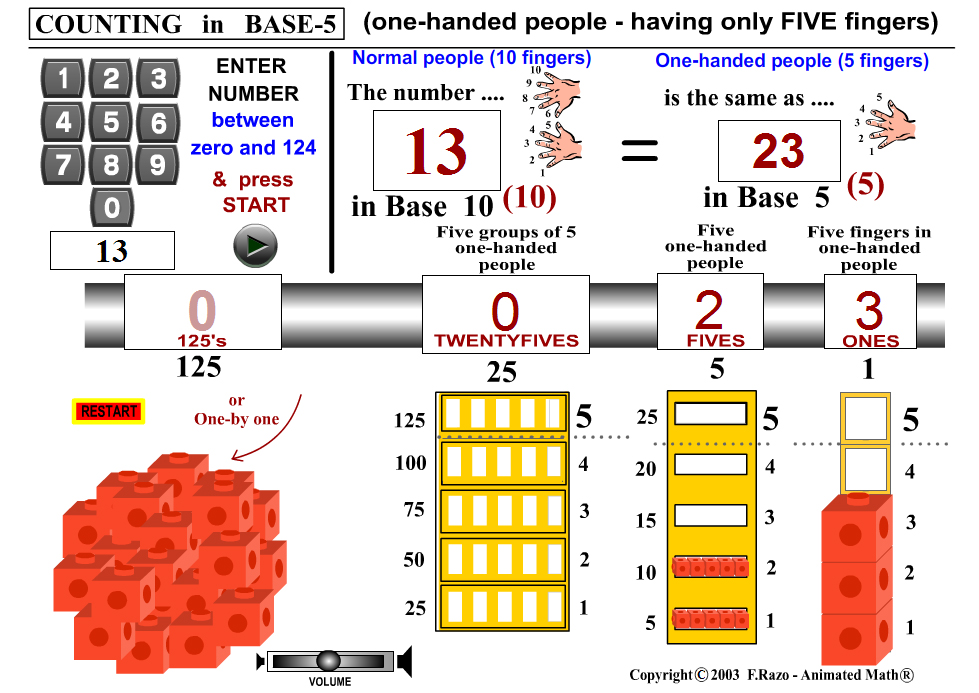
Grouping 13 Items different bases - by 10’s, 5’s, and 2’s

13 10 = 23 5 = 1101 2
 |
 |
 |
FRACTIONS
In the upper elementary grades, the topic of place value could extend to the representation of fractions
Fig 3 Representation of Fractional Parts in Bases 10, and 2 - The number 23.675
Below, an ancient Babylonian clay tablet, made some 4,000 years ago, is shown including symbols and calculations describing the relationship between the sizes of sides in right triangles, including fractional parts. The numbers, as stated in a Base 60 number system, correspond to calculation assumed to have been first stated in the "Pythagorean Theorem", some 2,000 years later. The activity on the right, titled "Inter Bases Converter", allows students to enter a number in Base 10, and display expanded (approximate) equivalent representations with fractional parts of up to 5 digits in two other arbitrary bases.
Fig 4 Equivalent Representation with fractional parts in Different Number Bases
ADDITION, SUBTRACTION, AND MULTIPLICATION
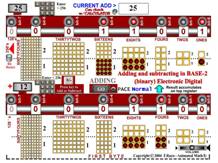
The process of addition of two numbers is shown below, step by step, using symbols, and visual virtual objects, in Base 10 and in Base 2. The activities provide multi sensory demonstration of digit-by-digit, place value by place value addition and regrouping of objects into larger bundles (carrying), highlighting the similarity of processes followed, regardless of the choice of base (i.e. bundle size).
|
|
|||
Fig 5 Addition in Bases 10, and 2
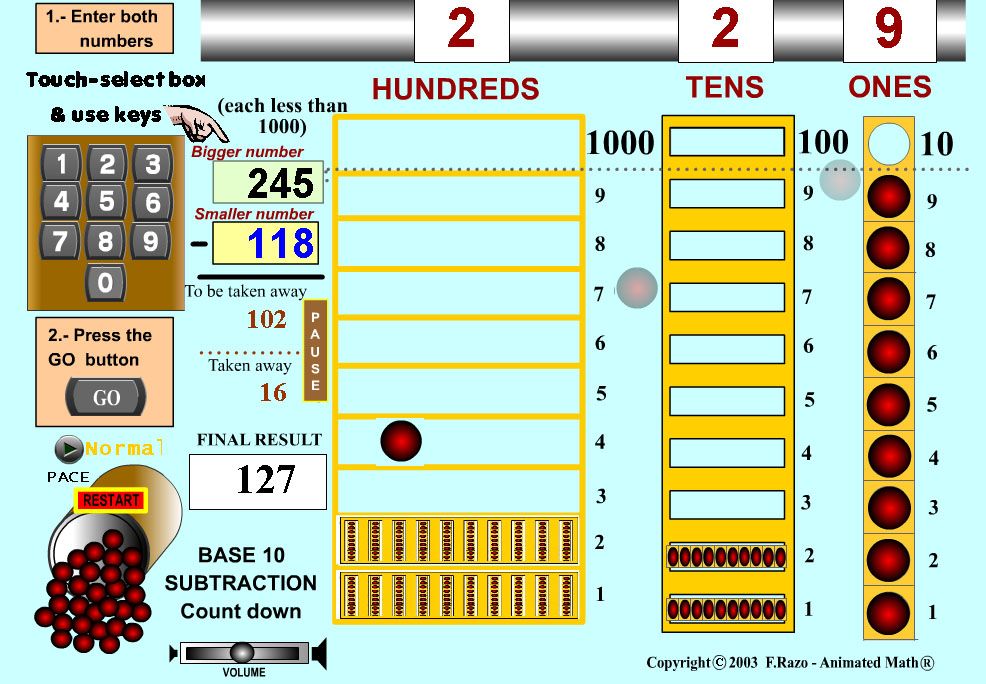
Subtraction in Base 10 is shown below as the undoing of addition. The first activity animates the undoing of groups using progressive unbundling (borrowing), while the second shows the overlaying of the undo-amount onto place-value groups. The third activity, Subtraction in Base 2 is used to show a highly effective process that converts numbers into a negative form called complement which when added, achieves equivalent subtraction. While this process could be used the same in any base, it has proven to be extremely simple and efficient when implemented in electronic binary arithmetic circuitry. Because of its significance, the topic of negative complements would need to be considered for further exploration with students, to include examples in Base 10. In the Subtraction in Base 2 activity below, the "+/-" key is used to show the conversion of the second number from an addend, to a subtrahend, by the simple reversal (flipping) of each binary digit (bit) to its opposite, or bit-complement (0 > 1, or 1 > 0), before adding it. In otherwords, there is no need for a dedicated "subtraction circuit", since an adder will do the same using simple complements. The group of 8 bits used in the Base 2 activity below are called a byte.
 |
 |
 |
Subtraction in Base 10 Counting backwards |
Subtraction in Base 10 Overlaying undo-amount |
Subtraction in Base 2 Using twos-complement |
Fig 6 Subtraction in Base 10, and in Base 2 - Using two's complements
The images in Figure 7 below are of activities that illustrate the standard, right-to-left process of multiplication, as taught traditionally to elementary grade children. The first activity shows an animation of the common, symbolic process in Base 10. The second presents a virtual simulation of the same process for Base 2, using pebbles, zeroes, ones and lights. The third activity mimics the standard Base 10 symbolic procedure but applied to binary digits. Presenting these similar processes together allows students to identify the similarities and power of the algorithms being learned. all the way into the workings of current Base 2 digital computers. Today's electronic digital computers do the same repeatedly, inexhaustibly, and at extremely fast speeds, using semiconductors, transistors, microcircuits and a variety of micro materials and electromagnetic processes.
Fig 7 Multiplication in Bases 10, and 2
THE PAST AND THE PRESENT
The images below are those of a Base 10 /decimal mechanical accounting machine (left) that was popular around the middle of the twentieth century (NCR Model 32, circa 1950) and next to it (center), the panel of an early, vintage electronic Base 2 /binary digital computer (DEC PDP-8, circa 1965), representing the face of the sweeping electronic technologies that came to replace mechanical computing. To the right are images of large scale integrated (LSI) binary circuit microchips, perhaps billions of times more powerful, and thousands of times smaller than their predecessors. The NCR Model 32 highlighted its ability to accumulate some 20 total numbers in its mechanical gears, and perform an addition in about one second. Today's microchips can hold billions of numbers, and additions within billionths of a second, with capabilities commonly increasing faster than suspected.
 |
 |
|
NCR Model 31 Decimal Mechanical Accounting Machine |
Fig 8 Images of mechanical and electronic tools used to automate basic arithmetic operations
BASES OTHER THAN TEN IN THE K-12 CLASSROOM
Informal field tests conducted in and out of the classroom, so far seem to point to feasible increases in interest, eagerness to understand, and improvement in performance in learning the basic concept of place value, even among lower elementay grade children. During classroom trials, virtual interactive activities have demonstrated their potential to support traditional, pedagogically proven approaches for teaching numeracy, both for the standard Base 10, as well as for other number systems. The inclusion of the Base 2 system and the fact that it is the one used in today's digital computers, usually arises extraordinary interest and motivation, in both younger and older students. More field trials are currently underway.
BIBLIOGRAPHY